Monty Hallova úloha

Aneb jedna z nejznámějších logických úloh na světě, která je velmi oblíbená v hodinách filosofie.

Představte si, že se zúčastníte televizní soutěže, jejíž hlavní výhrou je auto. To však nezískáte automaticky; poté, co se dostanete do finále, si máte vybrat jedny ze tří dveří. Dvoje z těchto dveří neskrývají nic, za jedněmi je vaše vysněná výhra. Pokud otevřete správné dveře, je auto vaše, pokud špatné, nezískáte nic. Jelikož nemáte žádnou nápovědu a u všech dveří je stejná pravděpodobnost, že skrývají hlavní výhru, je šance, že si vyberete správně, 33%.

Uvažujme nyní, že moderátor namísto odhalení, co se skrývá za vámi vybranými dveřmi, otevře jedny ze zbývajících dvou dveří (tedy ne ty vaše). Vy se tak dozvíte, že tyto dveře výhru neskrývají, a od moderátora nyní dostanete nabídku své původní rozhodnutí změnit. Pokud se rozhodnete zůstat u původních dveří, odnesete si v případě výhry navíc bonus $100, pokud svůj výběr přehodnotíte, žádnou odměnu navíc neobdržíte.

V názorném příkladu to tak může vypadat třeba tak, že si vyberete dveře č. 3 a moderátor následně otevře dveře č. 2. Teď již víte, že se hlavní cena skrývá za dveřmi č. 1 nebo dveřmi č. 3. Rozhodnete se změnit svou volbu a necháte si otevřít dveře č. 1, nebo zůstanete u svého původního výběru, tedy dveří č. 3? Pro vyloučení nějakých psychologických spekulací ještě dodejme, že moderátor možnost změnit dveře nabízí všem soutěžícím (tedy nehledě na to, jestli si vybrali poprvé správně či špatně) a že pro vás nabízených $100 představuje pouze sympatický bonus, váš hlavní cíl je totiž vyhrát auto.

Je správné zůstat u původní volby? Pokud ano, proč? Pokud ne, proč ne?

Logické (a správné) řešení

Autorem této hádanky je Marilyn vos Savant, žena s nejvyšším IQ na světě. Vymyslela ji pro jeden časopis v roce 1990 a jako správné řešení tehdy uvedla, že by soutěžící měl nabídky moderátora využít a volbu změnit. V následujících týdnech dostala od čtenářů kolem deseti tisíc dopisů, přičemž naprostá většina z nich se točila kolem toho, že nemá pravdu. Logika i počítačové simulace však ukazují, že pokud využijete moderátorovy nabídky, máte šanci na výhru 66%, kdežto pokud se rozhodnete zůstat u původních dveří, vyhrajete pouze ve 33% případů.

Vše se odvíjí od toho, že když si poprvé vybíráte "své" dveře, vaše šance na výhru je 1/3. Stejná pravděpodobnost přitom leží i na ostatních neotevřených dveřích. Když však moderátor jedny ze zbývajících dvou dveří otevře, šance, že tyto otevřené dveře skrývají auto, padá (logicky) na nulu. A oněch 33% se přesouvá na dveře, které si soutěžící nezvolil.

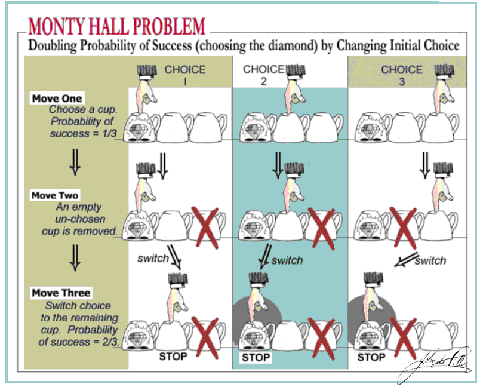
Pokud mi nevěříte a myslíte si, že po otevření jedněch dveří, je možnost najít auto za zbývajími dvěma 50:50, schválně se podívejte na tuto názornou a velmi jednoduchou ukázku. V prvním řádku můžete vidět svou původní volbu, která je úspěšná ve 33% případů, ve druhém možnost, kdy jsou jedny dveře odstraněny a vy názor nezměníte, a konečně ve třetím případ, kdy se po odstranění jedné špatné možnosti rozhodnete svou volbu přehodnotit.